小学学到的运算律是交换律、结合律、分配律。
它们非常重要,从现在开始,它们就要频繁使用在计算里了。
所以,孩子们必须理解透彻。
好,我们先说交换律。

一、交换律
说交换律之前,我们要先说[相等]。
等号,在数学中到底有什么样的意义呢?
孩子们会遇到比大小的题目。
比如说4+7与9+2谁大?
这里是要填“=”的。
那么相等意味着计算的结果相同吗?
4+7=11,9+2也等于11。
11与11相同,所以是相等的——这是我们普通意义上的理解。
其实,还有更深一层的意思。
一个数与另外一个数相等,就意味着它们在数轴上的点是重合的。
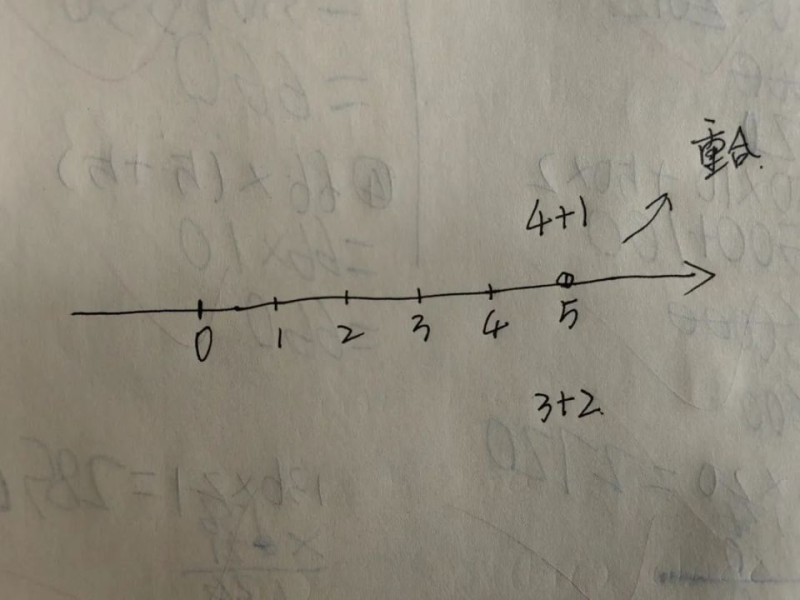
明白了这点,我们才好往下证明交换律。
现在:
1+5+6=12
6+1+5=12
我们把数字交换了位置,计算的结果是相同的。
我们就可以说加法有交换律吗?
不,这是先验的经验,不叫数学证明。
我们要假设任意数,a.b.c都符合。
看下面的数轴演示。
无论是a+b+c,还是a+c+b,交换位置后,最终在数轴上重合了(这里我们不能说相等了,因为没有明显的像11一样的表象相同)。
如此,我们才说加法符合交换律。
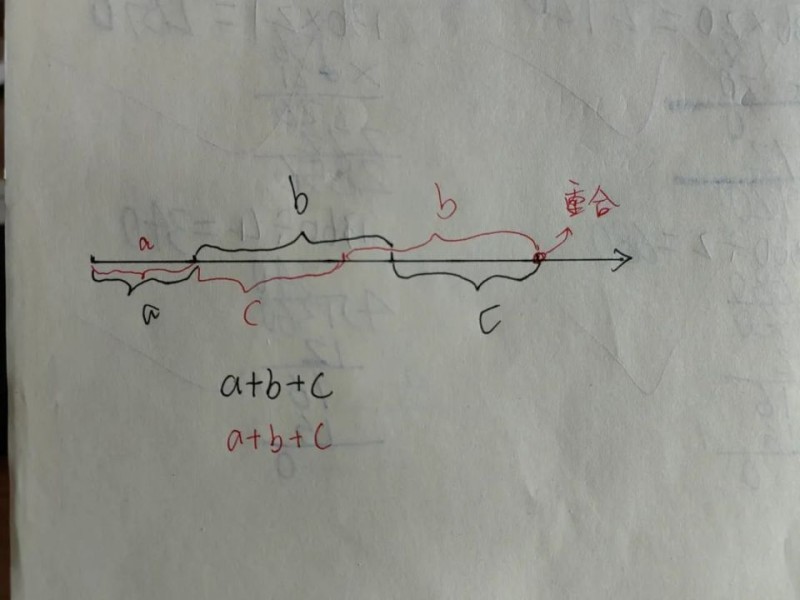
我们设的是ABC是任意数。
小学课本上ABC是自然数。
小学的数系只到自然数、分数、小数,基本上在正数的范畴内运算。
我们都知道还有负数,无理数、超越数……
那么,交换律对于这些数也是成立的。
拿负数举例子。
看下面的数轴演示。
无论我先加哪个数,最后的结果在数轴上都是重合的。
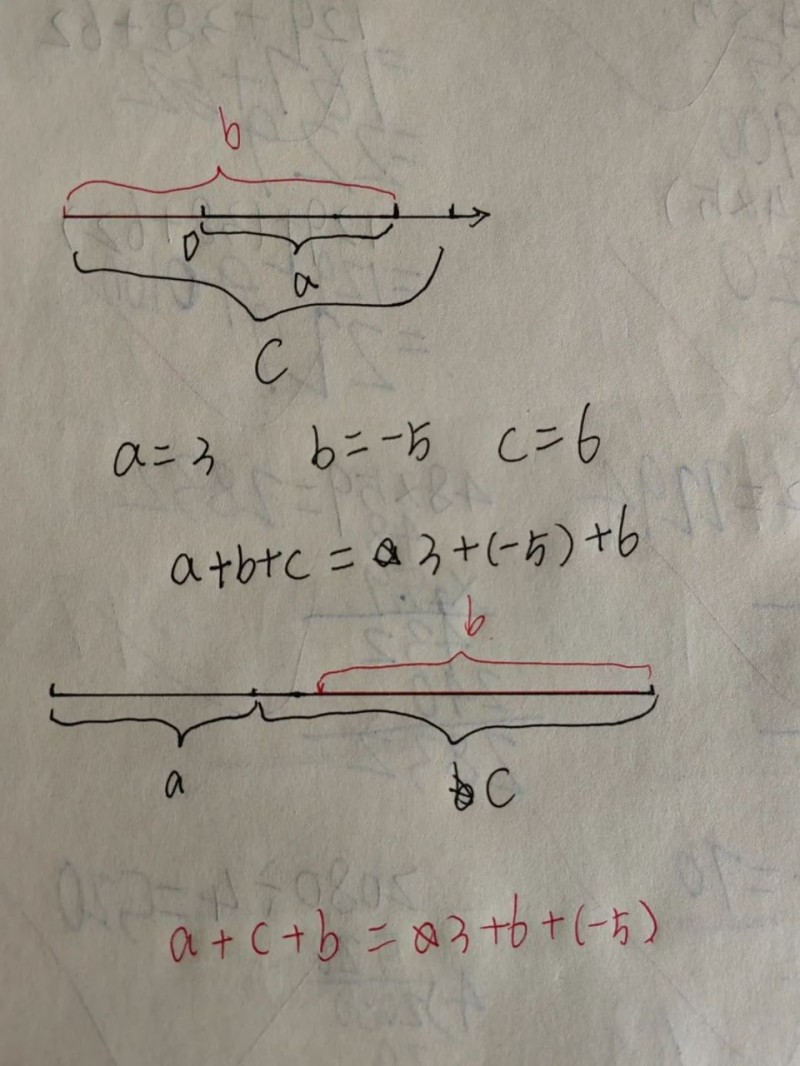
其实减法,加减混合,除法也是符合交换律的(最直观的你可以弄几个数试一试)。
只是我们不这样说。
到初中数系扩展之后,我们把前面带减号的都称为负数,负数之间的运算本质上也是加法运算。
一个定理的表达要简洁、覆盖更多的范围。
如果单说加法交换律,就能够把很多事情统一起来的话,我们就不需要引入其他的概念了。
说的太多,小学生是非常容易迷糊的。
到中学数系扩展之后会,会给学生们演示:
负数也符合交换律、
代数式也符合交换律、
无理数也符合交换律……
甚至到高中后:
虚数也符合交换律,
向量也符合交换律。
结合律、分配律都是如此。
只要是在有限的范围内,都适用。(无无限数列不适用)

到这里总结一下:
好,下面我们说乘法交换律。
乘法交换律很好说。
因为乘法就是加法——乘法是重复的加。
既然是重复的加,无非就是多加几次,本质上是一样的。
所以,乘法交换律不需要特别证明。
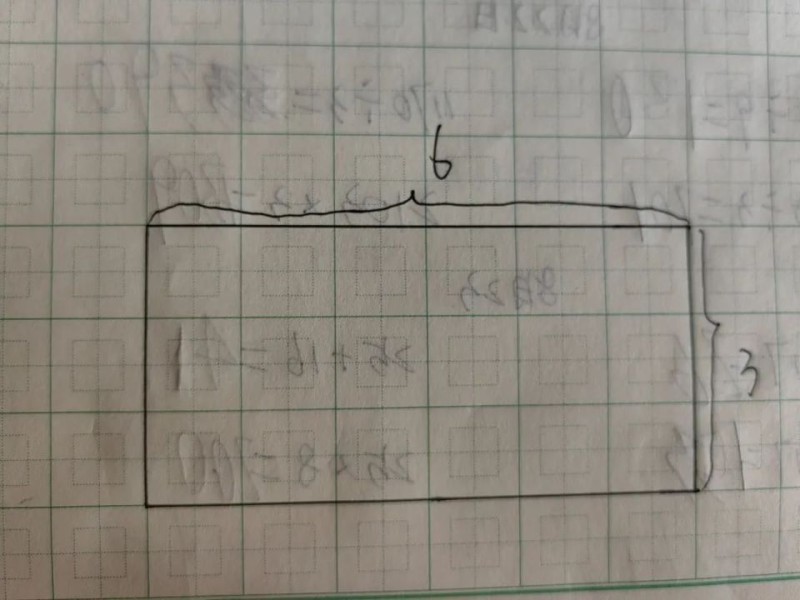
如果想给孩子讲的话,可画一个长方形。
它的边长是6和3。
用长乘以宽和用宽乘以长,它的面积还是这个面积。
这样很简洁。
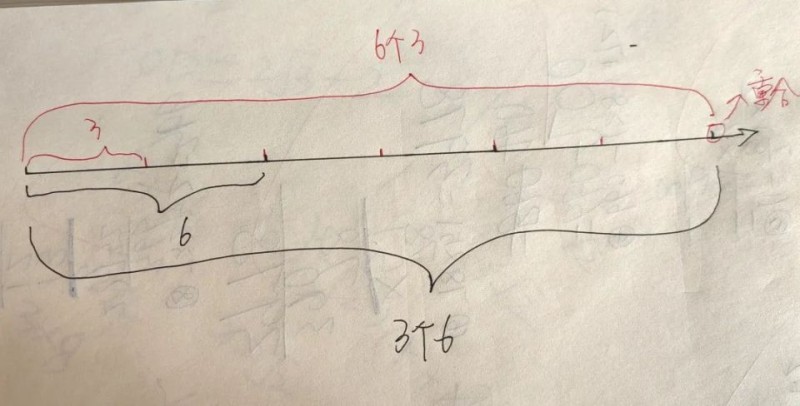
或者,你就在数轴上演示3个6和6个3(a个b与b个a),最后是重合的。
二、结合律
加法和乘法都有结合律。
a+b+c=a+(b+c)
也就是说给b和c加一个括号,整体算式的优先级变了。
先计算b+c。
没有关系,在数轴上演示一下。
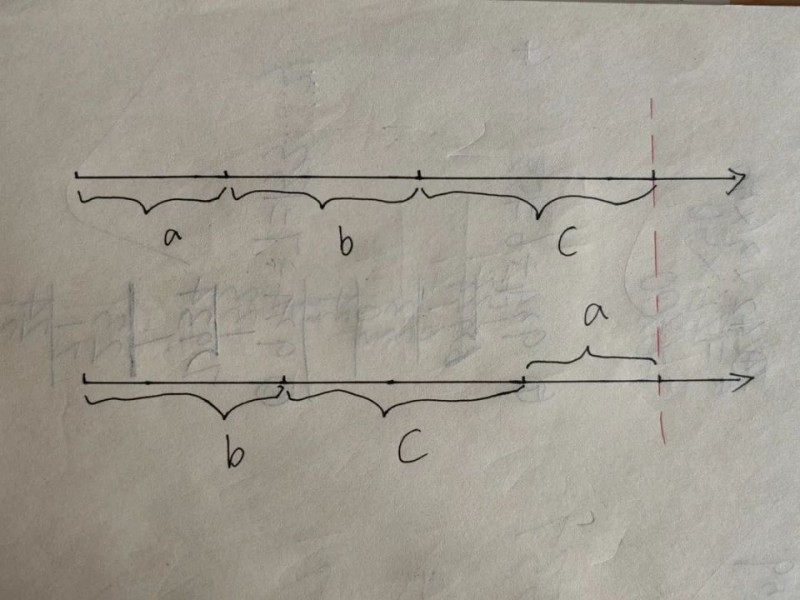
优先级换了后,其实就是计算顺序变了。
顺序变了,跟加法交换律换一换位值没有太大区别(说法上的不同)。
然而,在实际应用上造成的结果却很不一样。
68+53+47=168
68+(53+47)=168
计算简便程度不同。
乘法加上括号后,也是改变了优先级。
比如a×b×c与a×(b×c),从先算a×b换成了先算b×c。
那么a个b与b个c,先算哪个,在数轴上的结果都是重合。不再演示。
区别还是计算的简便度。
另外,我们用长方体演示一下(方便你给孩子讲解)。
一个长方体的体积是长×宽×高。
那我们翻转一下长方体,宽和高就变成了长和宽,长就变成了高——结合律的体现。
这一种方式比较适合给孩子说,但不是严格的结合律证明。
另外,减法和除法有结合律吗?
通常123-64-36,我们可以写成123-(64+36)使计算简便,但我们不说这是减法的结合律。
有的人叫它减法的性质,同理还有除法的性质。
比如600÷2÷5,可以写成600÷(2×5)。
换成实际的例子是:
我们可以算一共摘了几个,再用总数去减——123-(64+36),也可以一个一个减——123-64-36。
仔细揣摩一下,这也是结合律的体现,前面我们说过,所有运算本质上都是加法。
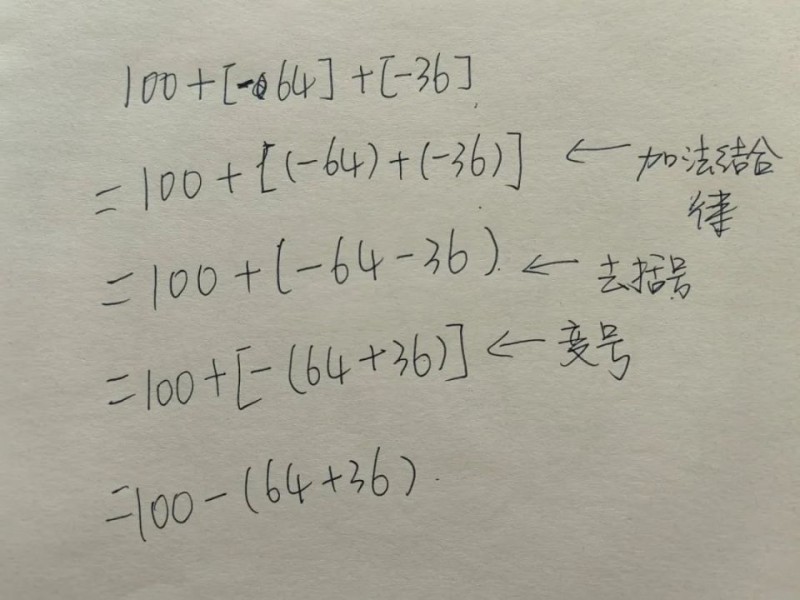

只是太麻烦了,我们不这样说。
这一点我们知道就行,在今后的运算中,会悟出来的。
小结一下:
三、分配律
加法为什么没有分配律了?只有乘法有?
看下面这个图,求长方形的面积。
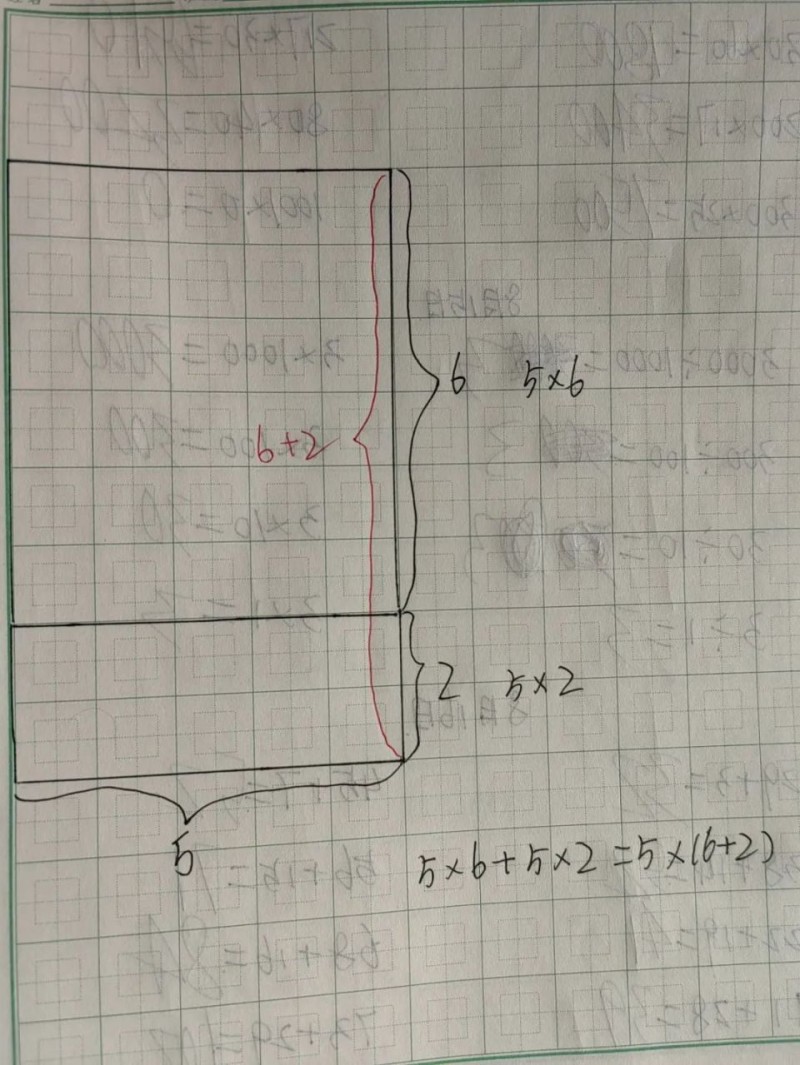
上图演绎了分配律。
它在加法里,不这样表达——每个小正方形的面积是1,用加法就是反复加。
所以,只有乘法,才有这样的表达。
分配律是乘法基于加法的延伸。
用长方形、正方形演示都可以。
还可以用乘法的本质来说明。
25×(4+8)=25×4+25×8
这里一共有12个25相加,我们可以4个25加上8个25.
按照这样的方式理解,分配律反过来正过来你都能用。
而且25×(15-7)你也知道如何分配。
15个25,减去7个25.
这就是学习为什么要抓住底层原理——
能帮你触达更多。

还有,除法有分配律吗?
有。
(600-400)÷2=(600-400)×½——可用乘法分配律。
(600+400)÷2=(600+400)×½——可用乘法分配律。
不过,还是那句话,中间还需要倒腾一步,不难为孩子们。
孩子们只需要记住加法、乘法交换律、结合律,乘法分配律。
将来的,将来再说。
小结一下:
四、目的
到这里,我们来说一下,使用运算律的目的是什么。
为了简便。
小学现在叫简便运算,我们使用的北师大版本,内容量不大,但是使用运算律,主要演练场景和计算诉求还是【简便】。
在这一点人教版的重视程度更高一些。
到初中、高中要使用代数式推理演绎。
那么长的代数式你如何理顺它、让它显现出【端倪】、方便你解题或者方便你解决实际问题?
使用运算律。
到时候不止有基础运算律,还有跟其他公式的配合使用。
所以,本质上就是为了方便,这一点跟孩子讲清楚。
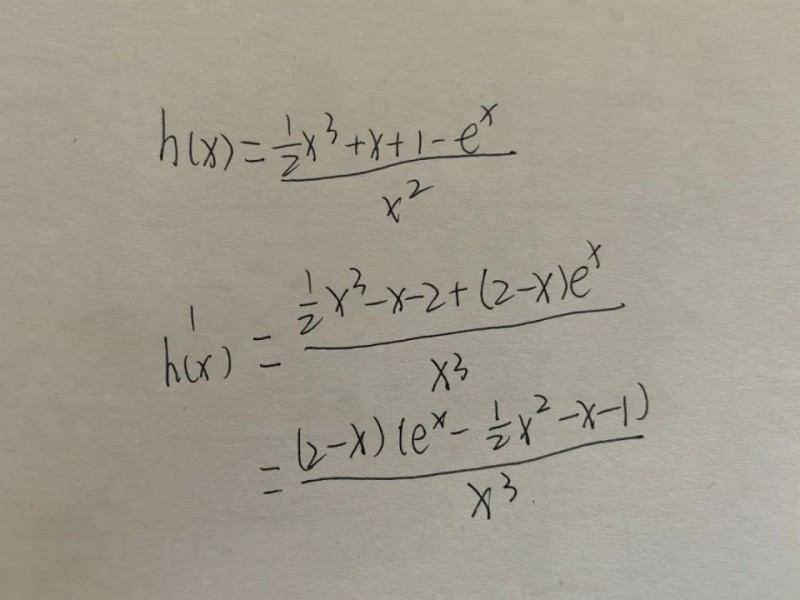
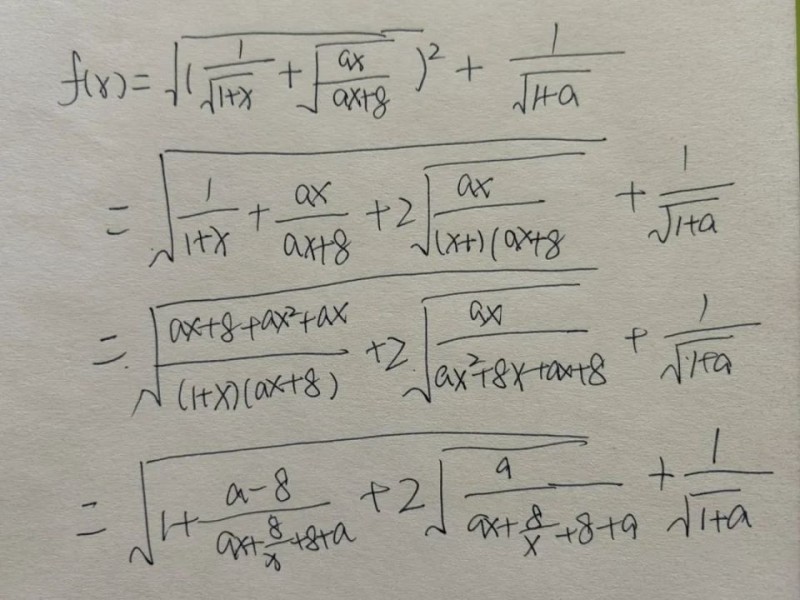
好,这就是今天的分享了。
有不成熟的地方,欢迎留言指正。
谢谢阅读,本文结束。
